犀牛曲面建模简单教程及曲面建模原理探究

犀牛曲面建模一直是犀牛学习的重点难点，同时也是设计师必须要攻克的常用建模技巧，对于曲面建模品索教育前面已经分享过不少rhino曲面建模教程，下面品索教育要分享的一个简单曲面建模教程的同时为你分享曲面建模的原理的探究，包括原理的思考，实例操作检测以及曲面建模原理的总结，如果你也还是对曲面建模存在不少疑问的话，那么下面这篇精彩的干货整理一定不要错过了！

我们先从一个简单的犀牛曲面教程看起：

1.在侧视图画一条曲线

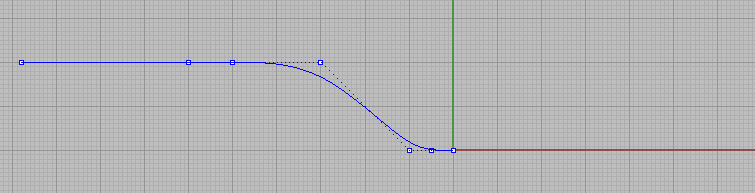
2.点击“记录构建历史”很重要

3.旋转成型（不要出错，出错要从第2步重来）

4.你是不是得到了这么一个东西呢？对凹陷不满意？没关系，继续往下看！

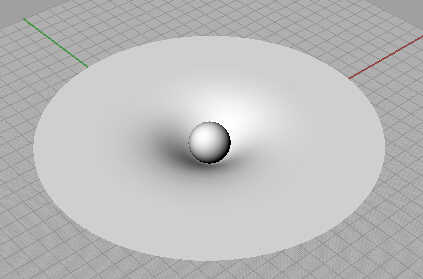
5.亮瞎的时刻到了！去调整第一步画的这个蓝线，凹面会同步变动！

6.最后拿个正方形分割下就好了。

犀牛曲面建模原理探究：

对象的精确数据定位是非常重要的。一条空间曲线，必须有很严谨的定义，必须从某个坐标开始定义清楚每个点。必须能够清楚这曲线上的每个点的方向曲率。这样，使用非常重要的sweep时才能得到可靠的结果。众所周知，从建筑学的角度看，是不允许出现含糊的工程数据的。

如果建筑对象是一个放养体，它就应该有严谨的数据。应该是截面形体沿着轨迹曲线运动时刻保持与切线方向垂直。可是。很糟糕，sweep允许形体并不在与切线垂直的平面上。这对建筑来说是致命的随意。而且如果起点没有保证垂直正交就会造成后续的偏移。

那么事实究竟如何？那就是必须将放样形体放在空间曲线的起点切线的垂直平面上保持准确的正交垂直关系，否则不能有确定精确的数据。

实例操作来验证：

1 输入命令Curve. 在front视图上画曲线。在top视图上调整。建立一条具有普遍性意义的空间曲线f1。

2 命令CrvStart，标记曲线的起点。开启点捕捉，中心点捕捉，最近点捕捉。

3 命令Curvature。绘制起点处的曲率圆。由曲率圆圆心和圆上一个最近点与曲线f1起点得到一个空间平面。由此平面得平面过圆心点法线。由此法线与f1起点建立平面F0.

4 命令Cplane. 在空间平面F0上绘制形体S1.形体经过f1的起点。

5 命令sweep1.得到实体A。

6 复制形体S1并在曲线f1起点曲率圆平面旋转一个角度，仍然经过曲线起点。Sweep1得到的实体B.比较 A与B并不相同。

7 在曲线的任意点上作一截平面，使用截平面trim掉一部分，使用DupEdge获得截面形体S2.

8 命令Length比较两个曲线形体S1与S2,完全相等。

9 实际的工程绘图应该将所有模型的位置从绝对坐标点（0，0，0）开始定义。这样，曲线f1的空间位置是严谨确定的。其内部特性也是严谨确定的。由此建立的sweep放样形体是严谨可靠的。这绝非skp，max可以比拟的。

结论：

犀牛确实是像cad一样严谨精确的优秀软件。它能够给模型的任意部分一个精确的数学性的交代。

1  我们所用到的一般的曲面都可以表达在完美的数学方程中F(x,y,z)=0.关于连续性可微性以及一系列复杂的曲面性质，有一套成熟完美的数学理论。可以这么肯定地回答，只有在数学理论中，曲面的完美性才能够得到透彻的揭示。

2 曲面就是由线编织的。就像布一样，大量的经线纬线密密麻麻结构成不同的曲面。从二维降到一维，如果不借助线来理解曲面，不知还有没有更好的办法。至少这是非常合乎人直觉习惯的办法。

3 模型曲面不同于数学家关注的数学曲面。数学家也会研究一个曲面F和一簇曲面F#。但模型曲面更多的像是一个模糊集合。在变化中保持不变的东西到底是什么呢？假如最初的曲面有一个确切的数学方程来表述，那么对设计师来说，这个方程绝不是用来限定思维的牢笼和不变量。

4 犀牛曲面是一种特定的多项式函数表达的曲面，就是所谓的Nurbs曲面。它根本的特点是保持局部的调整不牵涉整体的改变。与影视行业仅仅关注视觉效果而使用polygon建模不同，犀牛的数学确定性是工业制造的基础。